正三角形パズルを解くには？魔方陣の基本と小学生・中学生向けの解説？三角形魔方陣の解き方：小学生から大人まで楽しめる算数パズル

それでは、まず正三角形パズルについて見ていきましょう。

このパズルは、算数的な思考力を養うのに役立ちます。

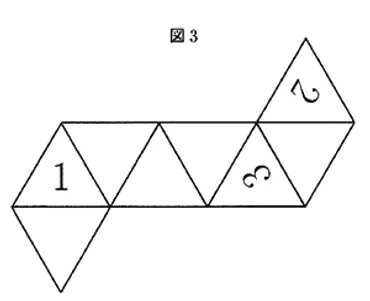
立体の正三角形パズル

正三角形パズルは、数字の配置と合計に着目することで、論理的思考力を養うのに適しています。

中学受験の算数にも関連していますね。

立体魔方陣とその展開図（開成中学２０１４年）どう解く？中学受験算数

✅ 1から8の数字が書かれた正三角形を組み合わせて立体を作り、頂点に集まる4枚の三角形の数字の合計が全て等しくなるように配置する。

✅ 問題では、頂点の数字の合計、辺の両側の三角形の数字の合計の比較、特定の数字が配置された場合の他の数字の配置などが問われている。

✅ 関連する算数パズルや中学受験算数の解法集を紹介するウェブサイトへのリンクが示されている。

さらに読む ⇒どう解く？中学受験算数出典/画像元: http://jukensansu.cocolog-nifty.com/blog/2014/11/post-8508.html

数字を組み合わせて立体を作るという点が面白いですね。

頂点の数字の合計が同じになるように配置するという条件も、パズルとしての面白さを増しています。

ある算数の問題として、1から8までの数字が書かれた正三角形を組み合わせて立体を作るパズルがあります。

この立体は、各頂点に4枚の正三角形が集まり、頂点の数字の合計が全て同じになるように構成されています。

このパズルでは、各頂点の数字の合計が18になることが求められます。

また、辺を共有する正三角形の数字の合計が等しいという特性も重要です。

例えば、三角形ABCに数字1が書かれている場合、数字8が書かれている可能性のある三角形は、三角形ACD、三角形AEB、三角形FBCの3つです。

なるほど、数字の配置と合計値のバランスが重要ですね。関連するウェブサイトへのリンクも、非常に参考になります。

三角形の魔方陣パズルの基本

三角形の魔方陣パズルの基本について解説します。

数字の合計によって解が存在するかどうかが変わってくる点が興味深いですね。

三角形の方陣算一辺

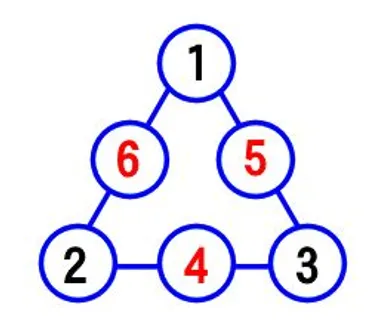
✅ 1から6の数字をそれぞれ1回ずつ使って、各辺の3つの数の和が9になるように配置する問題について、頂点の数の和が6になることから、頂点に1, 2, 3を配置することがわかる。

✅ 問題の解法として、数字の合計と辺の数の関係から、頂点の数字の合計を求める方法が示されている。

✅ 同様に、各辺の数の和を10にする場合の魔方陣についても触れられている。

さらに読む ⇒法人もりの学校トップページ出典/画像元: https://www.morinogakko.com/classroom/sansu/bunsyoumondai/houjinzan/sankaku9/a3.html

各辺の和が一定になるように数字を配置するパズル、面白いですね。

頂点の数字の合計によって解のパターンが決まる点が、論理的思考を促します。

次に、三角形の各辺の数字の合計を等しくする「三角形の魔方陣」パズルについて見ていきましょう。

このパズルは、1から6までの数字を1回ずつ使用し、三角形の各辺の数字の合計を等しくするというものです。

辺の合計（S）によって解の存在が変わります。

Sが9、10、11、12の場合は解が存在し、それぞれの頂点の数字が特定されます。

例えば、S=9の場合、頂点の数字の合計は6となり、(123)の組み合わせに限定されます。

S=10、S=11、S=12の場合も同様に、頂点の数字の組み合わせと辺の数字が決定されます。

しかし、Sが13以上になると解は存在しません。

数字の組み合わせで解が変わってくるのが、まるで政治の駆け引きのようで面白いですね！