正三角形パズルを解くには?魔方陣の基本と小学生・中学生向けの解説?三角形魔方陣の解き方:小学生から大人まで楽しめる算数パズル
数字パズルで脳トレ!正三角形を組み合わせて立体を作る算数パズルから、三角形の魔方陣まで、数字の配置で頭を悩ませる問題を解説。小学生から中学生まで楽しめる、数学的思考を鍛える奥深いパズルワールドへ!
小学生・中学生向けの解説と注意点
三角形魔方陣、頂点の数字の合計って、どうやって求めるの?
(S-7)×3 で計算できる!
小学生・中学生向けの解説では、数式を用いて頂点の数字の合計を求める方法が示されています。
理解を深めるのに役立ちます。
公開日:2017/09/21
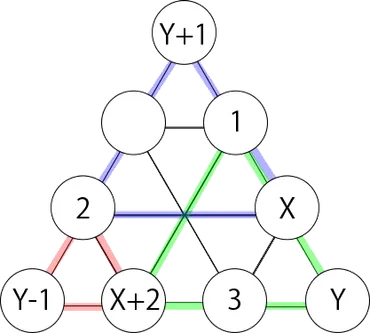
✅ 9つの点に1から9までの整数を入れ、正三角形の頂点の数の和を等しくなるようにする問題。
✅ ウに1、エに2、クに3を入れた場合、正三角形の頂点の和が15になるように各点に数字を割り振る。
✅ キに9が入ることが判明する。
さらに読む ⇒公務員試験数的処理解法テクニック出典/画像元: https://komaro.net/questions/kazu/mahoujin-hukumennzann/question3/小学生にも理解しやすいように工夫されているのが素晴らしいですね。
数式を用いることで、より深く理解できるようになる点も良いですね。
三角形の魔方陣パズルは、小学生にも理解できるような工夫がされています。
具体的には、数字の合計と頂点の数字の関係がわかりやすく説明されています。
中学生向けには、数式を用いてその関係性が詳細に解説されており、頂点の数字の合計 (X+Y+Z) は (S-7)×3 で表されます。
この数式を用いることで、辺の合計(S)と頂点の数字の関係を理解し、解を導き出すことができます。
このパズルは、教科書では「魔法の三角形」として紹介されることがありますが、数学的に解明できることから、この表現は必ずしも適切ではありません。
また、魔法陣と魔方陣は似た概念ですが、数学的な定義には違いがあります。
三角形の魔方陣は、小学生でも楽しめるように工夫されているんですね。数式を使って理解を深めることもできるなんて、すごい!
一辺4数字の三角形魔方陣
三角形魔方陣、辺の合計18と22に解がないのはなぜ?
頂点の数字の合計と辺の合計の関係で解けない。
一辺4数字の三角形魔方陣について解説します。
数字の組み合わせを考慮し、論理的に解を導き出すことが重要になります。

✅ 魔方陣は、縦・横・斜めの数字の合計が等しくなるパズルで、計算力と論理的思考力を養うのに役立ちます。
✅ 解法のポイントは、数が限定される箇所から考え、数字の組み合わせを考慮することです。
✅ 記事では、足し算と掛け算の魔方陣の解法が例題を通して解説されており、複雑な問題を解くためのヒントが示されています。
さらに読む ⇒トップページ出典/画像元: https://www.manabinoba.com/math/3185.html一辺4数字の三角形の魔方陣は、数字の組み合わせのパターンが多く、解を絞り込むのが難しそうですね。
Sの値ごとに解が存在するかどうかが変わるのも奥深いです。
次に、1~9の数字をそれぞれ1回ずつ使用する、一辺4数字の三角形の魔方陣について掘り下げていきます。
ここでは、辺の合計(S)が17 18 19 20 21 22 23の場合を考えます。
S=18とS=22には解が存在しません。
基本的な考え方は、一辺3数字の三角形魔方陣と同様で、頂点の数字の合計(X+Y+Z)と辺の合計(S)の関係式、(S-15)×3=X+Y+Z、を導き出すことです。
この関係式を利用して、各Sの値に対応するX+Y+Zの組み合わせを求め、数字の組み合わせを検討して解を絞り込みます。
一辺4数字の魔方陣は、さらに難易度が上がりそうですね。でも、解法を理解すれば、きっと解けるようになるはずです。
S=23とS=17の解法とまとめ
魔方陣パズル、S=23と17の解法、見つけるコツは?
組み合わせ試行錯誤と条件合致が鍵!
S=23とS=17の解法とまとめです。
魔方陣の奥深さを感じて頂ければと思います。
✅ 魔方陣(magic square)に関する内容で、様々なパターンの魔方陣の作成方法や、関連する計算方法などを説明しています。
✅ 魔方陣の例として、3×3の魔方陣が紹介され、縦、横、斜めの和が全て同じになること、そして、魔方陣の数字の並びにおける興味深い法則性について触れています。
✅ 魔方陣に関する用語や、魔方陣の性質、作成するための計算方法などを解説し、魔方陣の奥深さや面白さを伝えています。
さらに読む ⇒大同大学出典/画像元: https://www.daido-it.ac.jp/~oishi/TH5/ms.htmlS=23とS=17という具体的な例を通して、解法を詳細に解説している点が素晴らしいですね。
試行錯誤しながら解を求める過程は、パズルの醍醐味ですね。
具体的に、S=23の場合、頂点の数字の合計は24となり、(789)という組み合わせのみが可能です。
S=17の場合、頂点の数字の合計は6となり、(123)の組み合わせのみが可能です。
それぞれのSの値に対応する具体的な解の導出過程が示され、最終的な解答例が提示されています。
S=23とS=17の解を見つける過程では、数字の組み合わせを試行錯誤し、条件に合致する解を丁寧に探し出す必要があります。
これらの解法と考察を通じて、三角形の魔方陣パズルの奥深さを体験できます。
色んな解法があるんですね。私も色んな魔方陣を解いてみたいです!
本日の記事では、様々な三角形パズル、特に数字の配置と合計に着目した問題をご紹介しました。
算数パズルの奥深さを感じて頂ければ幸いです。
💡 正三角形パズル、魔方陣は数字の配置と合計に注目し、論理的思考力を養うのに役立ちます。
💡 小学生から大人まで楽しめる三角形魔方陣パズルは、様々な解法と奥深さを持っています。
💡 数字の組み合わせを理解し、解法を学ぶことで、算数パズルの面白さを体験できます。


